A Variance-Reduced and Stabilized Proximal Stochastic Gradient Method with Support Identification Guarantees for Structured Optimization
Abstract
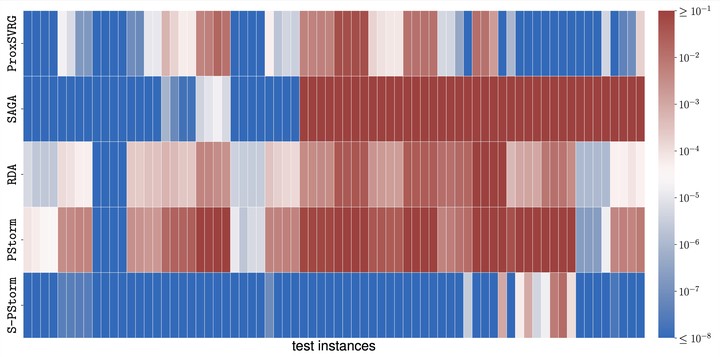
We propose, S-PStorm, a proximal stochastic gradient method with variance reduction and stabilization for structured sparse optimization. We prove an upper bound on the number of iterations required by S-PStorm before its iterates correctly identify with high probability an optimal support. Most algorithms with such a support identification property use variance reduction techniques that require either periodically evaluating an exact gradient or storing a set of stochastic gradients, while S-PStorm does not require either of these. Moreover, our support-identification result shows that, with high probability, an optimal support will be identified correctly in all iterations with the index above a threshold, while the few existing results prove that the optimal support is identified with high probability at each iteration with a sufficiently large index.